Dynamic lot size model
In inventory theory the Dynamic lot size model is a generalization of the economic order quantity model that takes into account that demand for the product varies over time. The model was introduced by H.M. Wagner and T.H. Whitin in 1958.
Problem setup
We have available a forecast of product demand 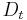 over a relevant time horizon (for example we might know how many widgets will be needed each week for the next 52 weeks). There is a setup cost
over a relevant time horizon (for example we might know how many widgets will be needed each week for the next 52 weeks). There is a setup cost  incurred for each order and there is an inventory holding cost
incurred for each order and there is an inventory holding cost  per item per period (S and H can also vary with time if desired). The problem is how many units to order now to minimize the sum of setup cost and inventory cost.
per item per period (S and H can also vary with time if desired). The problem is how many units to order now to minimize the sum of setup cost and inventory cost.
Wagner and Whitin gave an algorithm for finding the optimal solution by dynamic programming. Because this method was perceived by some as too complex, a number of authors also developed approximate heuristics for the problem.
External links
For more discussion on the mathematical model and constraints and a sample spreadsheet that uses forward dynamic programming visit Solving the Lot Sizing Problem using the Wagner-Whitin Algorithm
References
- H. M. Wagner: "Comments on Dynamic version of the economic lot size model", Management Science, Vol. 50 No. 12 Suppl., December 2004
- H. M. Wagner and T. Whitin, "Dynamic version of the economic lot size model," Management Science, Vol. 5, pp. 89-96, 1958